Near field and far field

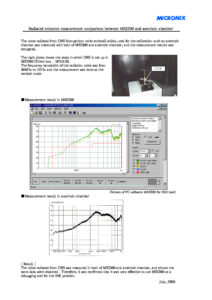
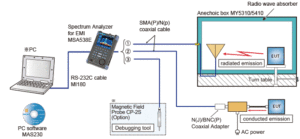
When the electric field strength and the magnetic field strength are measured, how much the distance between the transmission and the receiving antennas should be always becomes a problem. It is known well that the receiving in the far field is no problem.

Regarding a minute loop and a minute dipole, therefore, we consider where the borderline between the near field and the far field exists.

Minute loop

If only the electromagnetic field on the equatorial plane is threated, $$ \begin{cases} H=(πIS)/(λ^2D)\sqrt{ \ 1-(λ/2πD)^2+(λ/2πD)^4 } \\ E=(Z_0πIS)/(λ^2D) \sqrt{ \ 1+(λ/2πD)^2} \end{cases} $$

However, $$ \begin{cases} I&：\text{Loop current} \\ S&：\text{Loop area } \\ λ&：\text{Wavelength} \\ D&：\text{Distance between a transmission antenna and a receiving antenna } \\ Z_0&：\text{Impedance of free space(377Ω)} \end{cases} $$

1. Near field$(λ/2πD>1)$
2. The magnetic field strength H does not have any frequency depen dency because it does not contain the term of λ. Moreover, it is in inverse proportion to the third power of the distance. On the other hand, the electric field strength
3. E is in inverse proportion to the second power of the distance. H and E have a strong distance dependency, for instance, the ma gnetic field strength becomes 8 times if the distance becomes half.
4. Far field$(λ/2πD<1)$
5. The wave impedance is constant as follows:
6. The state of near field and far field is shown in Fig.1.
8. Fig.1:Electromagnetic field of minute loop

Minute dipole

$$ \begin{cases} H=(IL)/(2πD)\sqrt{ \ 1+(λ/2πD)^2 } \\ E=(Z_0IL)/(2πD) \sqrt{ \ 1-(λ/2πD)^2+(λ/2πD)^4} \end{cases} $$

However, $$ \begin{cases} I&：\text{Current flowing in wire} \\ L&：\text{Length of wire} \end{cases} $$

1. Near field(λ/2πD>1)
2. The wave impedance is in inverse proportion to frequency and distance as follows:
3. Far field(λ/2πD<1)
4. The wave impedance is constant as follows:
5. The wave impedance of minute loop and minute dipole is shown in Fig.2.
7. Fig.2:Wave impedence of minute loop and minute dipole
8. It is known from above that the borderline between the near field and the far field exists on the position of D＝λ/2π.
   
9. Moreover, the wave impedance completely becomes 377(Ω) from Fig.2 in case of D＝0.7λ, and this state can be called a far field. For instance, in case of 1GHz signal the position of 21cm or more is in a far field.

[Source]
Actual EMC design
tsutoshi Toba/supervision