電界強度及び磁界強度を測定する時、送信側と受信アンテナとの距離をどれくらいとればよいかが常に問題となる。遠方界で受信すればよいことは衆知である。
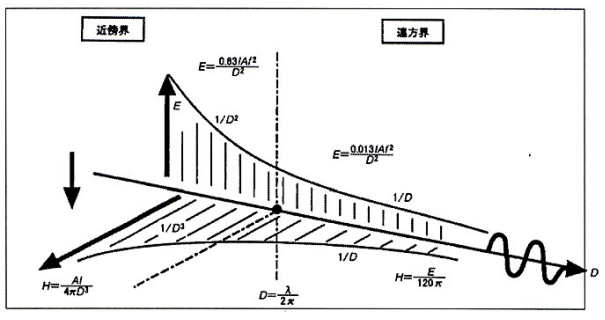
それでは近傍界と遠方界の境目がどこにあるかを微小ループと微小ダイポールについて考える。
微小ループ
赤道面上の電磁界のみを扱うものとすると、 $$ \begin{cases} H=(πIS)/(λ^2D)\sqrt{ \ 1-(λ/2πD)^2+(λ/2πD)^4 } \\ E=(Z_0πIS)/(λ^2D) \sqrt{ \ 1+(λ/2πD)^2} \end{cases} $$
ただし $$ \begin{cases} I&:\text{ループ電流} \\ S&:\text{ループの面積} \\ λ&:\text{波長} \\ D&:\text{送信側と受信アンテナの距離} \\ Z_0&:\text{自由空間インピーダンス(377Ω)} \end{cases} $$
- 近傍界\((λ/2πD>1)\)
$$ \begin{cases} H=(IS)/(4πD^3) \\ E=(Z_0IS)/(2λD^2) \end{cases} $$
磁界強度Hは、λの項を含まず、周波数依存性がない。また、距離Dの3乗に反比例する。
一方、電界強度Eは周波数に比例し距離の2乗に反比例する。
近傍界では距離依存性が強く、例えば磁界強度では距離が半分になれば磁界強度は8倍になる。 - 遠方界\((λ/2πD<1)\)
$$ \begin{cases} H=(πIS)/(λ^2D) \\ E=(Z_0πIS)/(λ^2D) \end{cases} $$
波動インピーダンスは
$$E/H=Z(377Ω)$$
で一定になる。
近傍界と遠方界の様子を図1に示す。
微小ダイポール
$$ \begin{cases} H=(IL)/(2πD)\sqrt{ \ 1+(λ/2πD)^2 } \\ E=(Z_0IL)/(2πD) \sqrt{ \ 1-(λ/2πD)^2+(λ/2πD)^4} \end{cases} $$
ただし $$ \begin{cases} I&:\text{ワイヤに流れる電流} \\ L&:\text{ワイヤの長さ} \end{cases} $$
近傍界(λ/2πD>1)
$$ \begin{cases} H=(IL)/(4πD^2) \\ E=(Z_0ILλ)/(8π^2D^3) \end{cases} $$
遠方界(λ/2πD<1)
$$ \begin{cases} H=(IL)/(2λD) \\ E=(Z_0IL)/(2λD) \end{cases} $$
波動インピーダンスは $$ E/H=Z_0(377Ω) $$
で一定になる。
微小ループと微小ダイポールの波動インピーダンスを図2に示す。
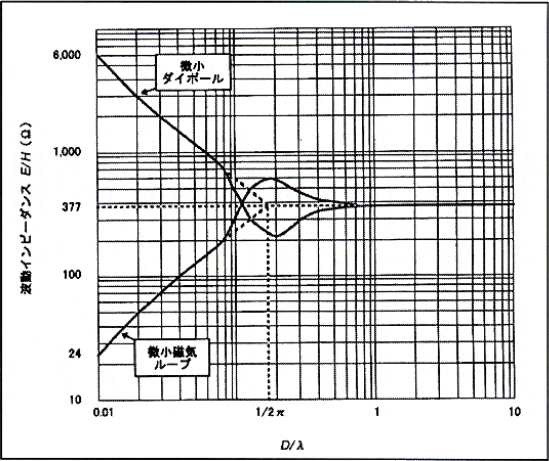
以上より、近傍界と遠方界の境目は、D=λ/2πにあることがわかる。また、図2からD=0.7λであれば波動インピーダンスが完全に377Ωとなり、遠方界と言える。例えば、1GHzの信号では21cm以上離れれば遠方界となる。
出展
EMC設計の実際
丸善株式会社 鳥羽光俊 監修

お気軽にお問い合わせください
見積もりが欲しい、電波暗箱をカスタマイズしたい、製品の修理がしたい。
どんな小さなこともお気軽にお問い合わせください。
(営業時間:8:30~17:30)