- 1. ETC/DSRCにおけるπ/4 QPSKの信号処理
- 1.1. ETCシステムのイメージ
- 1.2. 高速道路の各種アンテナ
- 1.3. 料金情報のやりとり
- 1.4. アダプティブスロッテドアロハ方式の全二重通信例
- 1.5. 通信トランザクション
- 1.6. DSRC規格
- 2. 送信系回路
- 2.1. π/4 QPSK変調回路
- 2.2. 信号空間ダイヤグラム(コンスタレーション)
- 2.3. 送信側FPGAブロック図
- 2.4. 絶対位相アドレス化
- 2.5. 差動符号化
- 2.6. マッピングテーブル
- 2.7. FIRフィルタ
- 2.8. 送信系RF回路
- 3. 受信系回路
- 3.1. 受信系RF回路
- 3.2. 受信側FPGAブロック図
- 3.3. 受信側全体タイミング図
- 3.4. FCMSフォーマット
- 3.5. 入力データRX I/Q DT[0-7]の内容
- 3.5.1. キーテクノロジー
- 3.6. 位相変換
- 3.7. クロック再生&定常位相誤差検出ブロック図
- 3.8. 位相連続化処理
- 3.9. π/4 傾き補正
- 3.10. 定常位相誤差検出
- 3.11. 定常位相誤差傾き補正
- 3.12. ゼロクロス検出
- 3.13. シンボルクロック作成
- 3.14. 差動複合化
- 3.15. AFC
- 3.16. 逆マッピング
- 3.17. π/4QPSKボード
- 4. 製品紹介
ETC/DSRCにおけるπ/4 QPSKの信号処理
ETCシステムのイメージ
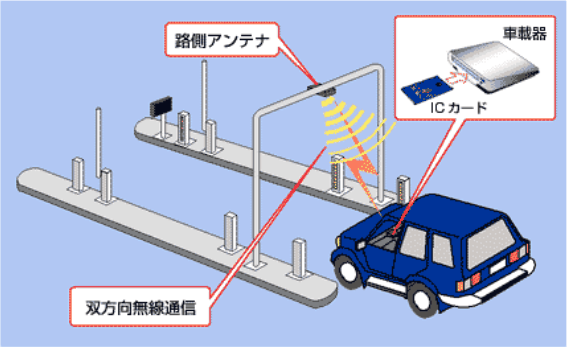
高速道路の各種アンテナ
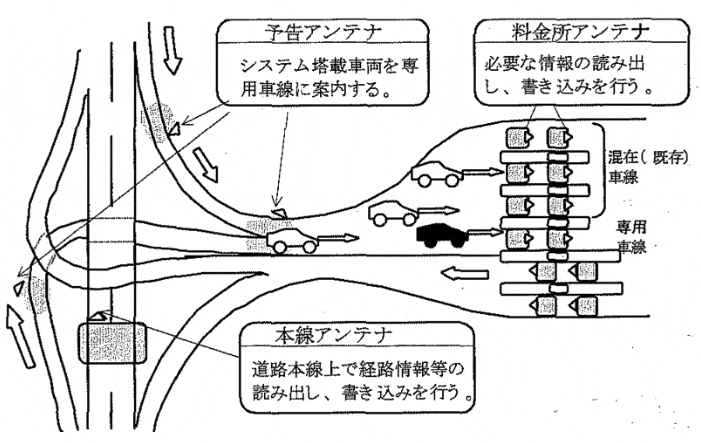
料金情報のやりとり
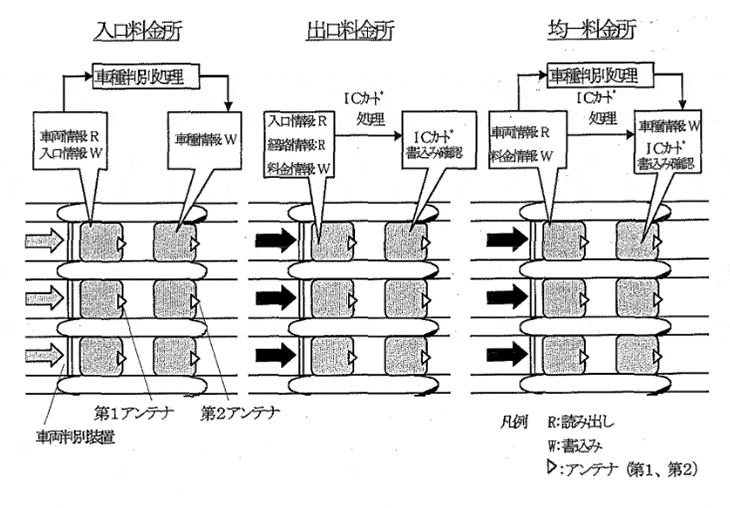
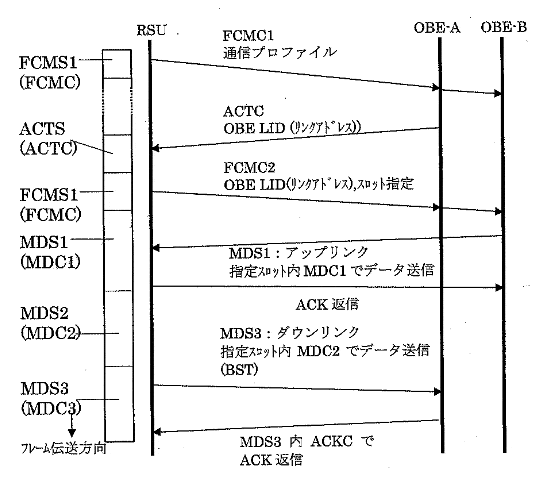
アダプティブスロッテドアロハ方式の全二重通信例
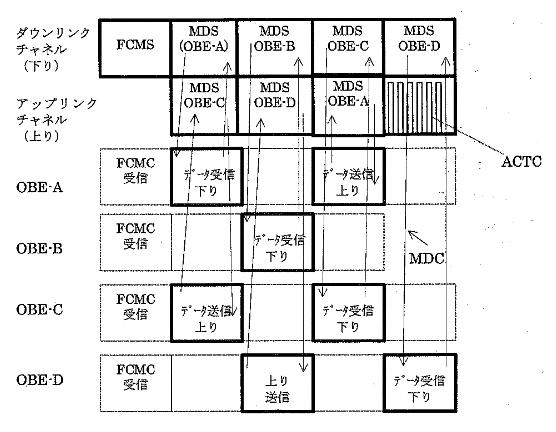
- FCMS:フレームコントロールメッセージスロット
- MDS:メッセージデータスロット
- ACTC:アクチベーションチャネル
通信トランザクション
DSRC規格
| 項目 | ASK方式 | QPSK方式 |
|---|---|---|
| 無線アクセス方式 | TDMA-FDD(多重数8以下) | |
| 周波数帯 | 5.8GHz帯 | |
| キャリア周波数間隔 | 40MHz | |
| 変調方式 | ASK | π/4QPSK |
| 変調速度 | 2.048Mbps | 2.048Mbps |
| データ伝送速度 | 1.024Mbps | 4.096Mbps |
| 符号化方式 | スプリットフェーズ符号 | 差動符号化 |
| 空中線電力 | RSU:300mW以下、但し伝播距離30m以下では10mW以下 OBE:10mW以下 試験機:1mW以下 | |
送信系回路
π/4 QPSK変調回路
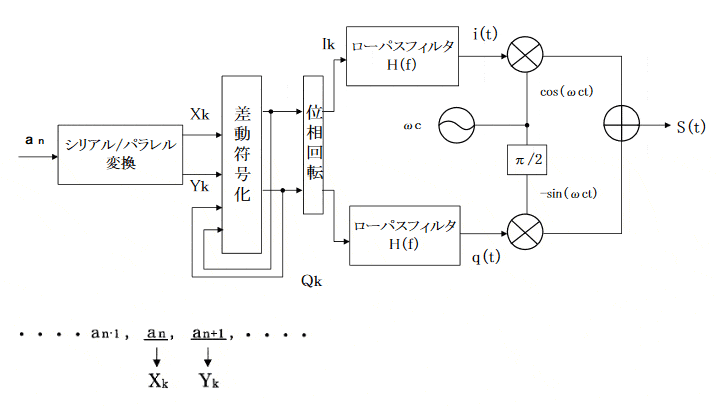
(Ik-1+jQk-1)にexp(jΔΦ(Xk, Yk)を乗算して位相回転し、同相と直交に分解。
Ik=Ik・1COS{ΔΦ(Xk, Yk)}-Qk・1sin{ΔΦ(Xk, Yk)}
Qk=Ik・1sin{ΔΦ(Xk, Yk)}-Qk・1cos{ΔΦ(Xk, Yk)}
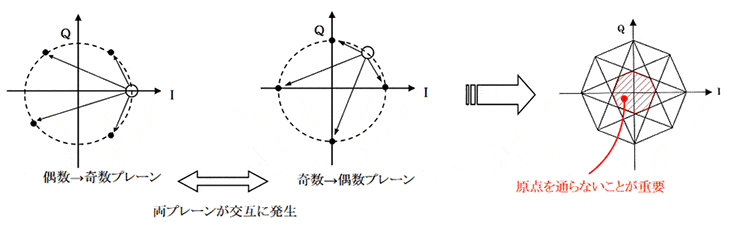
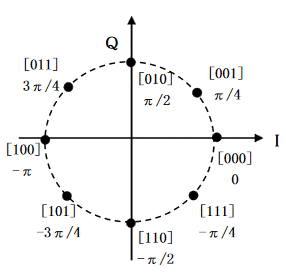
信号空間ダイヤグラム(コンスタレーション)
| Xk | Yk | Δ Φ |
|---|---|---|
| 0 | 0 | π4 (π/4) |
| 0 | 1 | 3π4 (3π/4) |
| 1 | 0 | -π4 (7π/4) |
| 1 | 1 | -3π4 (5π/4)M |
※赤文字:分子が奇数に注目
$$ (現位相)+(∆Φ:奇数)=\begin{cases} 奇数@現位相:偶数\\ 偶数@現位相:奇数 \end{cases} $$
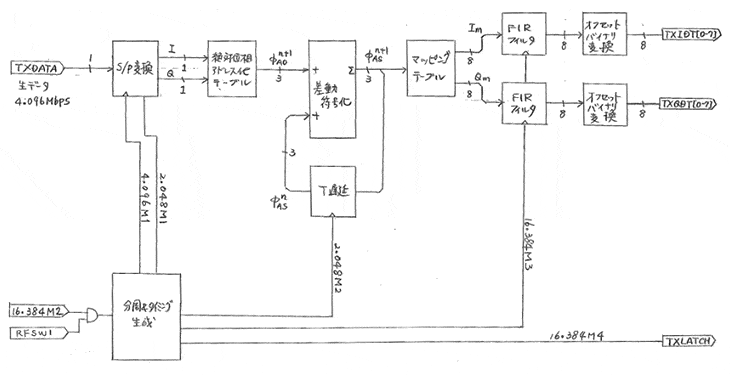
送信側FPGAブロック図
絶対位相アドレス化
| I | Q | ΔΦ | 絶対位相アドレス |
|---|---|---|---|
| 0 | 0 | π/4 | 001 |
| 0 | 1 | 3π/4 | 011 |
| 1 | 0 | -π/4 | 111 |
| 1 | 1 | -3π/4 | 101 |
差動符号化
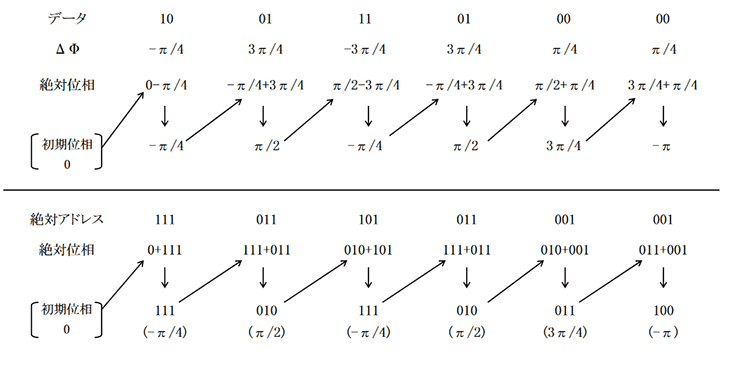
マッピングテーブル
- 位相データをImとQm振り幅に変換する。
- 振り幅は後段のFIRフィルタを考慮し、2‘s complement」表現とする。
| 位相データ | Im | Qm |
|---|---|---|
| 000 | 1 | (7F) |
| 001 | $$ 1/\sqrt{2} $$ | (5A) |
| 010 | 0 | (00) |
| 011 | $$ -1/\sqrt{2} $$ | (A6) |
| 100 | -1 | (80) |
| 101 | $$ -1/\sqrt{2} $$ | (A6) |
| 110 | 0 | (00) |
| 111 | $$ 1/\sqrt{2} $$ | (5A) |
【例.1】1→127(7F)とする $$ -1/\sqrt{2}→-\frac{127}{\sqrt2}=-90→A6@2'S comp. $$
FIRフィルタ
◆ベースバンド帯域制限にはナイキスト特性H(f)を用いること。(占有周波数帯幅と隣接チャネル洩電力と関係) $$ |H(f)|= \begin{cases} 1@0≦|f|<(1-α)/2T \\ cos^2[(T/4α)(2π|f|-π(1-α)/T]@(1-α)/2T≦|f|<(1+α)/2T \\ 0@(1+α)/2T≦|f| \end{cases} \\ \quad \\ 但し、=\begin{cases} T=1/2048×10^{-3}(s)=488.3(ns) \\ α=1 \end{cases} \\ \quad \\ ∴ \\ |H(f)|=\begin{cases} cos^2(0.7666×10^{-9}×|f|)@0≦|f|<2.048MHz \\ 0@|f|≧2.048MHz \end{cases} $$
※2's complementから後段のD/A変換機を考慮してオフセットバイナリーに変換する。
送信系RF回路
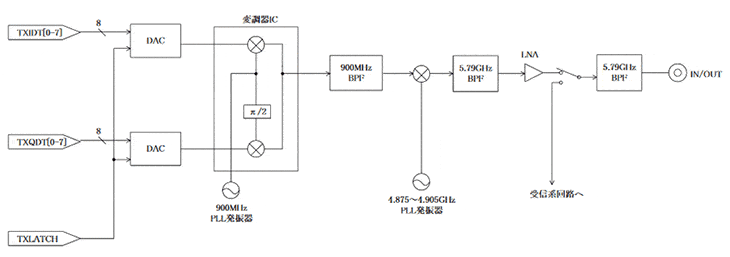
- 出力:5.775~5.805GHz(5MHzステップ)、-1dBm
- 変調器のミキサーは、入出力(IF入力/RF出力)間の振り幅が比例していること。
受信系回路
受信系RF回路
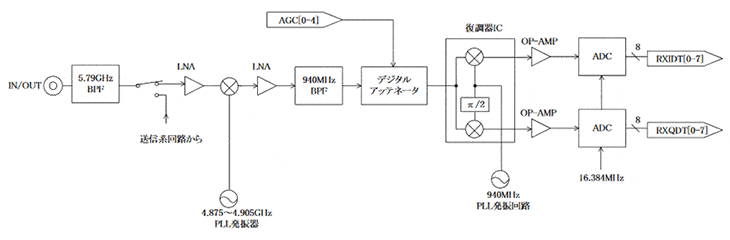
- 入力:5.815~5.845GHz(5MHzステップ)、-57~-25dBm
- 復調器ICのミキサーは、入出力(RF入力/IF出力)間の振り幅が比例していること。
受信側FPGAブロック図
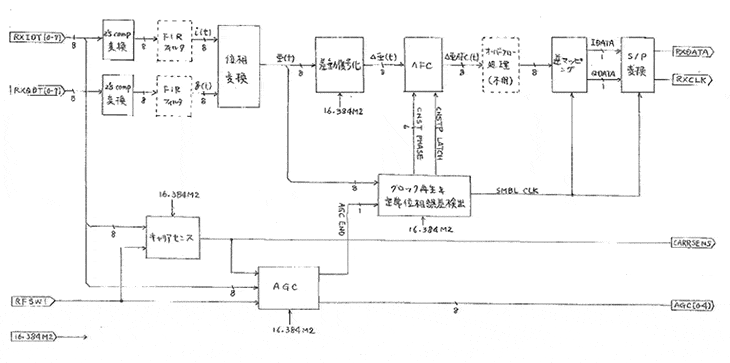
受信側全体タイミング図
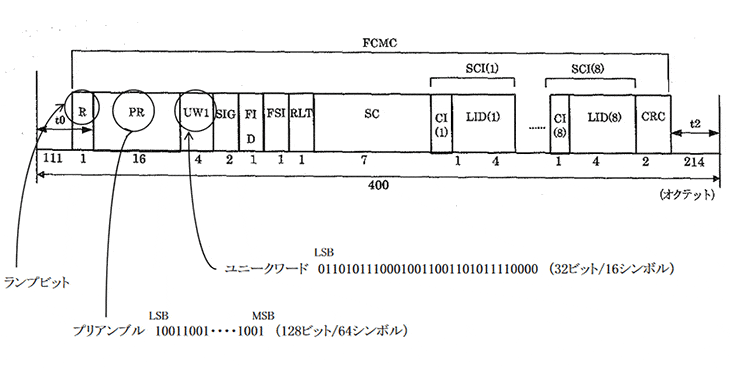
FCMSフォーマット
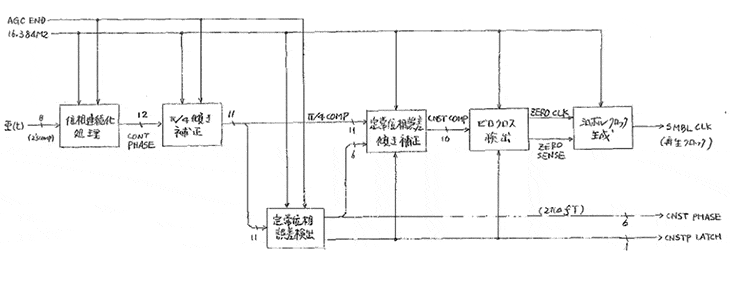
入力データRX I/Q DT[0-7]の内容
$$ ・RXIDT[0-7]=cos(θ^n_m(t)+2πΔft+Φ) \\ ・RXQDT[0-7]=sin(θ^n_m(t)+2πΔft+Φ) $$
$$ \begin{cases} θ^n_m(t)&:n番目の位相データ \\\quad\\ Δf&:受信搬送波周波数と本器の受信側ローカル周波数との差\\ &(2πΔft:定常位相誤差) \\\quad\\ Φ&:受信搬送波と本器の受信側ローカル発振起との位相差\\ &(少なくとも1スロットの間は一定値とする) \end{cases} $$
キーテクノロジー
- クロック再生
- 2πΔftの削除
- Φの削除
位相変換
$$ \begin{cases} RXIDT[0-7]@2's comp.=cos(θ^n_m(t)+2πΔft+Φ)=i(t) \\ RXQDT[0-7]@2's comp.=sin(θ^n_m(t)+2πΔft+Φ)=q(t) \end{cases} $$
位相変換ではΦ(t)を求める $$ \begin{align} Φ(t)$&=θ^n_m(t)+2πΔft+Φ \\ &=tan^{-1}(q(t)/i(t)) \\ &=Φ_0(t)+S(t) \end{align} $$
- \(Φ_0(t)\)
\(0≦Φ(t)<π/2\) において \(tan^{-1}(|q(t)/|i(t)|)\) テーブルを使う。\(0→00_H、π/2未満→3F_H\)(テーブル出力6ビット、その後\(00\)を上位に付加)
- \(S(t)\)
象限決定テーブルによる上位2ビットの決定
| 象限 | i(t)MSB | q(t)MSB | S(t) |
|---|---|---|---|
| 第1 | 0 | 0 | 00H(0) |
| 第2 | 1 | 0 | 40H(π/2) |
| 第3 | 1 | 1 | 80H(-π) |
| 第4 | 0 | 1 | C0H(-π/2 |
- \( Φ(t)\)
\( -π(80_H~0(00_H)~π未満(7F_H)\)
クロック再生&定常位相誤差検出ブロック図

位相連続化処理
Φ(t)=θnm(t)+2πΔft+Φ
2πΔft=Φ=0 とすると;
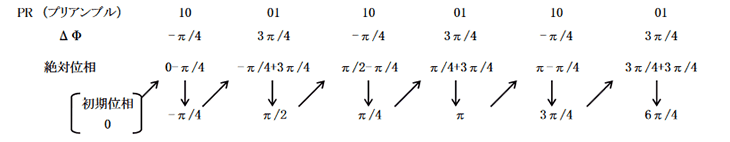
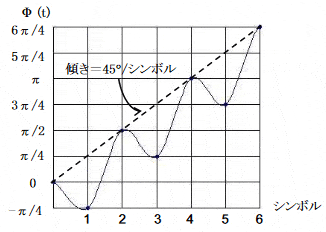
[PR:10101010・・・]により45°/シンボル傾きの波形が得られる。
◆ただし、上図よりさらにシンボルを増やしていくと位相の折り返しが発生し不連続となる。
連続化するためには次の処理を追加する必要がある。
- 初期補正量:0
- -π→+πへの変化時:(前補正量)-2π
- +π→-πへの変化時:(前補正量)+2π
π/4 傾き補正
Φ(t)は45°/シンボルの傾きがあるのでこれを補正する。
傾き式={(π/4)/8(クロック/シンボル)}× nΔt
=4nΔt(∵π→80H(128))
Δt =1/16.384MHz
傾き補正後波形=(位相連続処理後波形)-(傾き式)
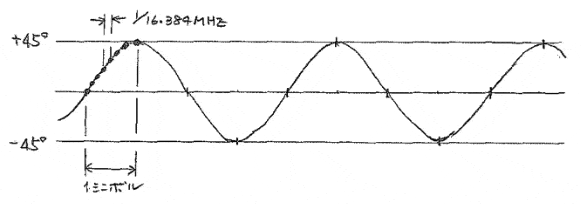
π/4傾き補正後の位相波形(2πΔft=0)
定常位相誤差検出
本回路では1シンボル(T)当たりの定常位相誤差2πΔfTを求める。
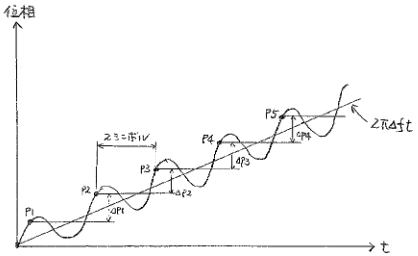
定常位相誤差に帰因する位相変化
2シンボル毎の振幅差ΔP(ΔP1~ΔP4の平均値)=2πΔf(2T)
∴ 2πΔfT=ΔP/2
- 2πΔfTの範囲 $$ \begin{cases} 送信側(車載器)周波数安定度=±20ppm \\ 受信側(試験機)周波数安定度=±5ppm \end{cases} $$
2πΔfT=±2π×(5.8GHz×25ppm)/2.048MHz
=±0.1416π(±25°)
定常位相誤差傾き補正
前段で検出された2πΔfTをもとに定常位相誤差2πΔfTを補正する
2πΔfT={(2πΔfT)/8(クロック/シンボル)}×nΔt.
Δt=1/16.384MHz
傾き補正後波形=(傾き補正前波形)-2πΔft
ゼロクロス検出
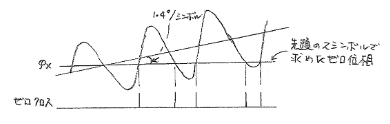
PR(プリアンブル)データから求めた連続位相波形は、2シンボルで1周期の波形である。するとゼロクロス点が1シンボル毎となる。
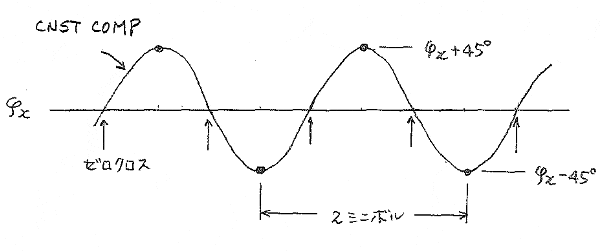
Φxの求め方:1周期である2シンボル分(16クロック)を加算(積分)すればよい。
シンボルクロック作成
ゼロクロス点と内部2.048MHzとをカウンタで同期させる。
問題点1:定常位相誤差傾き補正しても1シンボル当たり±1LSB(±1.4°)の誤差がある。
問題点2:位相波形が上下非対称だとシンボルクロックの周期が異なる。
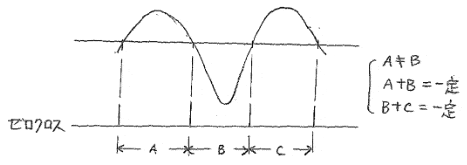
【対応】
ZERO SENSE 直後のZERO CLK(2シンボル分)の立上がりで内部2.048MHz(16.384MHzを8分週するカウンタ)に同期させる。
差動複合化
送信側では現シンボル位相に1つ前のシンボルの位相を加算しているので、受信側は引算する。
- 8クロック遅延
1シンボル8クロックなので1つ前のシンボルのデータは8クロック前のデータとなる。 - 不要位相のキャンセル
位相データ Φ(t)=θnm(t)+2πΔft+Φ- 2πΔftについて
(現シンボル)-(1つ前のシンボル)=2πΔftn-2πΔftn-1=2πΔf(tn-tn-1)=2πΔfT
差動複合化によって時間関数から一定値(2πΔfT)になる。後段のAFCでキャンセルする。 - Φについて
(現シンボル)-(1つ前シンボル)=Φ-Φ=0
差動複合化によってキャンセルされる。
- 2πΔftについて
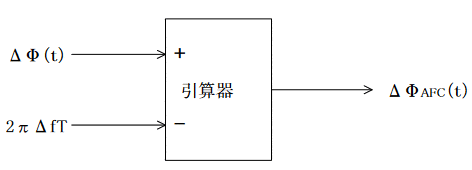
AFC
2πΔftは差動複合化で一定値2πΔfTに変換される。
2πΔftは定常位相誤差検出で求められた値である。
逆マッピング
本回路の入力には、差動符号化規則の位相データが入力されているのでこれを(I,Q)データに変換する。
| I Q | 位相データ |
|---|---|
| 1 1 | $-\frac{3}{4π}$ |
| 0 1 | $\frac{3}{4π}$ |
| 0 0 | $\frac{π}{4}$ |
| 1 0 | $-\frac{π}{4}$ |
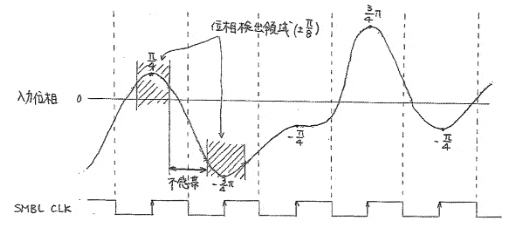
SMBL CLKの立上りで入力位相をLATCHし、そのデータが位相データの±π/8であればそれを位相データとする。
不感帯(π/4相当幅)を設けているのでこの区間では入力位相がどのように変化してもよい。
特にA/D変換器からのI,Q値が小さいときは位相変換後のΦ(T)は誤差が大きいが、この不感帯領域内であれば問題ない。
π/4QPSKボード
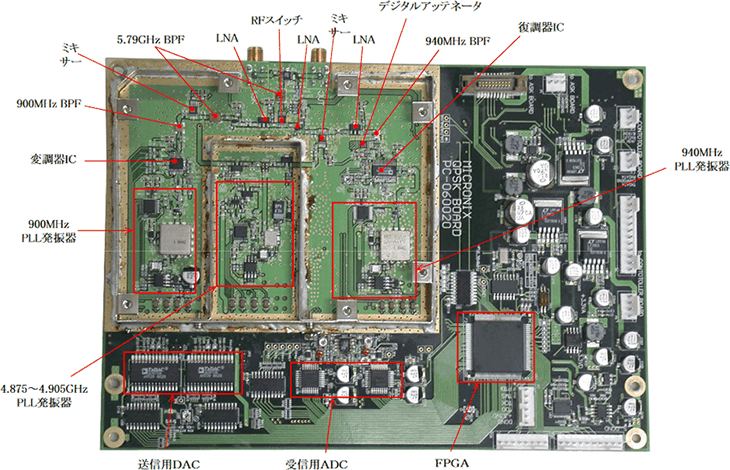
製品紹介
ETC/DSRCシステム
ETC/DSRC試験システムとテスタのリーディングカンパニー。ETC及びDSRC用試験システムは、料金所に設置された路側機(RSU)や車両に搭載される車載器(OBE)を自動的に試験。他にハンディ型のETC/DSRCテスタもラインアップ。

お気軽にお問い合わせください
見積もりが欲しい、電波暗箱をカスタマイズしたい、製品の修理がしたい。
どんな小さなこともお気軽にお問い合わせください。
(営業時間:8:30~17:30)


